Ernst Stueckelberg came up with many of the most fundamental ideas in 20th century theoretical physics but got little recognition. I learned about him when I realised that an evolution equation I derived from philosophical musings was introduced by him already in 1941. Stueckelberg was a modest man who struggled with life.

Ernst Stueckelberg was born in Basel in 1905. His mother Alice belonged to an aristocratic German family. That explains his impressive but cumbersome full name: Johann Melchior Ernst Karl Gerlach Stückelberg von Breidenbach zu Breidenstein und Melsbach.
When Alice’s father died, Ernst inherited the title Baron Souverain of the Holy Roman Empire of the Teutonic Nations of Breidenbach at Breidenstein and Melsbach. Ernst’s father Alfred was a lawyer, and his family had been citizens of the canton of Basel since the 14th century. Alfred gave his son a strict upbringing, seemingly to live up to his noble maternal heritage.
After obtaining his Ph.D. in physics in Basel at the young age of 22, Ernst was offered to come to Princeton as a research associate. There he applied the recently invented quantum mechanics to analyse the properties of molecules. The American physicist Philip Morse recollects [1]:
I also came to know a rather stiff young man, tall and thin, with an aristocratic profile and a Prussian manner and carriage. […] We came to be close friends, perhaps because opposites attract. [… He] could not help his name, nor could he help his mannerisms, which had been drilled into him by his father. He once told me his father would not allow him to take off his coat or tie even when he was studying by himself in his own room.
One of Stueckelberg’s achievements at Princeton was to explain the continuous spectrum of the hydrogen molecule H2. Later in life he expressed pride that this feat got it into the New York Times.
Available accounts differ on the order of events, but it seems that the Depression forced Princeton to let Stueckelberg go [2]. Back in Switzerland he could only get a job as a poorly paid Privatdozent.
Ernst married in 1931. Not long afterwards he seems to have lost a considerable wealth that belonged to his wife in naïve investments. To earn their living, Stueckelberg was forced to enlist in the army.
The pressing circumstances may have contributed to the fact that Stueckelberg began to express symptoms of mental illness around this time. These problems would haunt him for the rest of his life. His condition has been described as manic-depressive psychosis. He was often balanced and brilliant, but from time to time he had to retreat to the asylum for a few weeks.
The financial situation improved in spring 1935, when Stueckelberg was promoted to professor at the University of Geneva. When he returned to Europe, he had abandoned molecular physics and started working in the quickly developing fields of quantum theory and elementary particle physics.
Nevertheless, he was quite isolated, partly because of his personal situation. This is illustrated by the fact that between 1935 and 1943 Stueckelberg published 42 papers, 40 of which as the sole author.
He didn’t travel much and published most of his work in the local journal Helvetica Physica Acta, which was not widely read in the international physics community, partly because the articles were written in French.
His main lifeline to the scientific world was his friend Wolfgang Pauli, who, on the other hand, was central to the world of theoretical physics in the early to middle 20th century.
During fits of depression, Stueckelberg repeatedly submitted resignation letters to his university. They were always ignored, except once. In 1950 he had to be reinstated as professeur honoraire.
Despite his hardships, Stueckelberg came up with several groundbreaking ideas and results [3]. Some of them went unnoticed until they were rediscovered by others several years later. At least three of these ideas led to Nobel prizes – but not to Stueckelberg. Here are some examples of his achievements:
- In 1934, Stueckelberg devised a relativistically invariant perturbation method for quantum fields that preserves the gauge invariance of the full equations. It was mostly ignored. In retrospect, these general properties would have made his scheme suitable as a starting point to understand the divergences that plague perturbation expansions in quantum field theory.
- In 1935, he developed a model where nuclear forces were mediated by exchange particles (bosons), in a similar way as electromagnetic forces are mediated by photons. Stueckelberg dropped the idea since Pauli thought it was ridiculous. The idea was rediscovered by Yukawa, who got the Nobel prize for this work in 1949.
- In 1938 Stueckelberg discovered a special case of the Higgs mechanism that provides mass to the nuclear exchange particles he postulated in 1935. The corresponding Higgs particle was discovered in the LHC accelerator at CERN in 2013. Peter Higgs and François Englert received the Nobel prize the same year for their theoretical prediction of the particle.
- In 1941, he proposed the law of conservation of baryon number. Very simply speaking it says that matter can be transformed, but it cannot appear or disappear – just like energy.
- In 1941, Stueckelberg proposed that antiparticles may be seen as particles travelling backwards in time, an idea later utilised and popularised by Feynman. In doing so, Stueckelberg introduced a novel evolution equation that separates two aspects of time. This equation is the reason I learned about Stueckelberg (see postscript).
- In 1943, he outlined the idea of renormalisation to come to terms with the divergences to infinity that plague quantum field theory. Stueckelbergs’s paper was rejected by Physical Review as too sketchy. Later, Schwinger and Feynman published their version of the idea, which was more detailed and contributed to their Nobel prize in 1965.
- Stueckelberg’s work on renormalisation was formalised in 1953 together with the mathematician Andrée Petermann, with whom Stueckelberg discovered the renormalisation group. It expresses in general terms the effects of a scale change on the description of a physical system. Kenneth Wilson was awarded the Nobel prize in 1982 for his work in this field, which has wide-ranging applications, including phase transitions and critical phenomena in thermodynamics.
- Heisenberg came up with the idea of the scattering matrix (S-matrix) to represent the probabilities that initial sets of particles transform into other sets of particles. He hoped that the S-matrix could be used as a fundamental description of the microscopic world, thus getting rid of the mathematical problems associated with interacting quantum fields. Stueckelberg and Feynman independently published useful perturbation recipes based on the S-matrix programme in 1949. The two approaches are basically equivalent. Feynman illustrated his method by means of the famous Feynman diagrams of particle reactions.
A few weeks after receiving the Nobel prize in 1965, Feynman gave a lecture at CERN outside Geneva. Stueckelberg attended. Afterwards, Stueckelberg was making his way out alone from the amphitheatre. Feynman, surrounded by admirers, made the remark [4]:
“He did the work and walks alone toward the sunset; and, here I am, covered in all the glory, which rightfully should be his!”
Research and teaching seem to have been the focus of Stueckelberg’s life – perhaps like clear, calm lakes in the messy and troubled landscape of life. He didn’t seek recognition and seemed uninterested in administration, or in building a research group around his own ideas.
According to colleagues and students, Stueckelberg had a peculiar and careful style of writing and teaching. He is known for the generality and depth of his ideas, but also for idiosyncratic notation and convoluted expression. Therefore, his work was sometimes hard to understand and appreciate – even for highly gifted colleagues like Pauli.
Wolfgang Pauli was a harsh critic of the work of other physicists, Stueckelberg included. According the their colleague Konrad Bleuler: “[F]or Pauli, a lecture hall was a kind of a holy place where only truth was allowed. And a wrong statement was a sacrilege.” Bleuler recalls [5]:
“Stueckelberg always knew really special — I might say prophetic — ideas. He gave a lecture and of course Pauli — it happened very often — didn’t agree. And said ‘you are not allowed to say such things.’ But you see, Stueckelberg being a prophet, he’s not so easily stopped uttering his prophecies. So Pauli in despair menaced Stueckelberg with a stick and it seemed — I was not present myself but I was told — that the seminar ended like the war of Troy, Pauli, rather corpulent, with his stick after Stueckelberg around the table in the lecture hall.”
Stueckelberg’s health deteriorated in the 1960s. Electroshocks and experimental medication for his mental illness slurred his speech and sometimes affected his thinking. Crippled by arthritis, he was carried to seminars in the arms of younger colleagues [2].
He brought his dog Carlo III to his lectures and often talked to the animal about the subject at hand. Some claimed that the dog seemed to understand tensor calculus, since it barked when Stueckelberg made an error at the blackboard. The sceptic part of the audience suspected that the dog rather reacted to the hesitation of his master when he was about to commit a mistake.
In the final part of his life Stueckelberg embraced the Roman Catholic Church. He turned away from quantum theory and elementary particles to study relativistic thermodynamics. That subject may have had existential significance to Stueckelberg as it relates to the arrow of time. He devoted an entire book to it. According to fellow Swiss physicist Charles Enz [6]:
“[H]is book on thermodynamics makes arduous reading, defying the traditions of pedagogy, language, and notation. It is a logical construct without compromise, a cathedral of the spirit erected to prove with the aid of the notion of entropy that the time of physics is indeed the ‘biblical time’ having a beginning and an end, and not the ‘Greek time’ that flows uniformly from an infinitely distant past to an infinitely distant future.”
Stueckelberg had to end an interview a few months before his death because he was tired [2]. He painfully lifted himself out of his chair with two canes. A heavy gold cross dangled from his thin neck. “I look forward every day to my eventual journey to Heaven”, he said. “We live too long.”
Postscript
Here I describe how I came into contact with Stueckelberg and his work. In so doing I sketch some of my own ideas relating to time.
I pursue the idea that it should be possible to reconstruct the structure of physical law from epistemic principles. To this end, it is assumed that the structure of knowledge and the structure of the world reflect each other. A thorough analysis of what can be know about the world and what cannot provides lessons about the world itself.
According to this idea, one-to-one correspondence should appear between fundamental forms of appearances and the degrees of freedom in proper physical models. Here, the term forms of appearances is understood in the Kantian sense as categories of perception that are given a priori, into which all sensory impressions and all other elements of consciousness are placed.
Time is such a form of appearance. Kant viewed time as an essential such form, stating that it is a necessary representation that grounds all intuitions.
We can actually separate two aspects of the temporal form of appearance. The most basic one is the perceived flow of time, the directed sequence of events. This aspect of time may be parametrized by the variable T. On top of that we can measure temporal distances between events. Such distances may be expressed by means of the variable t. At each point in time T, which we may call now, we have knowledge of temporal distances t between an entire set of events, stretching from the present arbitrarily far back into the past. Of course, we may also know about the spatial distances between these events. Therefore, an entire space-time
$(x,y,z,t)$can be associated to each T, representing the known spatio-temporal relations at the present point in time. From the assumed epistemic perspective, the variables T and t should be treated as independent degrees of freedom in our physical models, even though they are related. From more careful considerations of this kind, it is possible to derive a quantum mechanical evolution equation
$i\hbar\frac{\partial}{\partial T}\Psi(x,y,z,t,T)=R \Psi(x,y,z,t,T)$where R is some Hermitean operator. This equation corresponds to the Schrödinger equation with a second temporal variable. The temporal metric is contained in t, meaning that relativistic transformations apply to t, but not to T. This makes the above evolution equation relativistically invariant, in contrast to the Schrödinger equation.
A few years ago I learned that Stueckelberg had arrived at the same equation already in 1941. He did not start out with philosophical musings like I did, but with his well-known desire for symmetry and relativistic invariance.
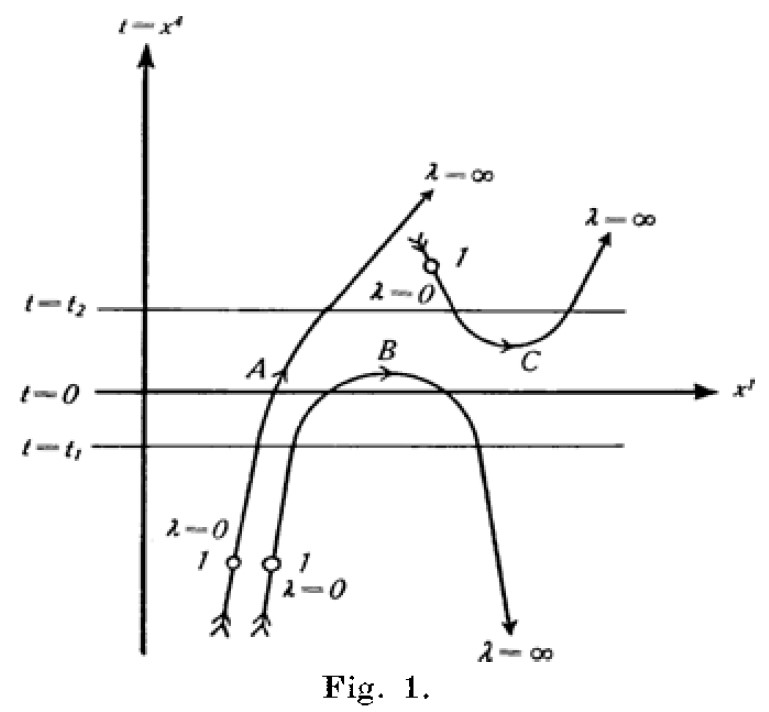
Stueckelberg used the evolution parameter T to be able to create particle trajectories that bended backwards in time t. He interpreted such trajectories as the creation or the annihilation of a particle-antiparticle pair, according to the figure below (taken from Ref. [7]).
The weakness of Stueckelberg’s approach is that he never provided any physical motivation for the introduction of the evolution parameter (which he called λ).
From the subjective point of view, it is very natural to unfold the now, represented by a given value of T, into an entire temporal axis t. Suppose that you listen to music. The appreciation of harmonies, and the emotional response they give rise to in the present, depend crucially on memories of sounds in the immediate past, and their metric intervals, to the extent that the music would cease to exist without these memories. That is, each present state of the listener contains both the present and the past in a crucial way.
At the formal level of physical description, the very perception of a sound at a given moment T relies on sensory recording during an extended period of time t, since such a temporal interval is needed to determine the frequencies that define the sound that we hear at a given moment. The same goes for spatial perceptions, since they arise when light with different frequencies enter the eye.
References
[1] Philip M. Morse, In at the Beginnings: A Physicist’s Life (MIT Press, 1977)
[2] Robert P. Crease and Charles C. Mann, The Second Creation, pp. 140-144 (Macmillan, 1986)
[3] Jan Lacki, Henri Ruegg, and Gérard Wanders (eds.) E. C. G. Stueckelberg, An Unconventional Figure of Twentieth Century Physics (Birkhäuser, 2009)
[4] Jagdish Mehra, The Beat of a Different Drum: The Life and Science of Richard Feynman, pp. 573-577 (Oxford University Press, 1994)
[5] Lillian Hoddeson, Interview with Konrad Bleuler, January 20, 1984 (Transcript by American Institute of Physics)
[6] Charles P. Enz, Ernst Stueckelberg, obituary, Physics Today 39(3), pp. 119-121 (1986)
[7] Ernst Stueckelberg, Remarque à propos de la création de paires de particules en théorie de relativité, Helvetica Physica Acta 14, pp. 588-594 (1941)

